Nuclear Magnetic Resonance in magnetic materials

1. Resonance is measurable without external magnetic field. Due to the internal magnetic field - characteristic of magnetically ordered materials - the nuclear energy levels are split without the application of the external field;
2. Very high resonance frequency. Very large hyperfine fields at the nuclei yield very high NMR frequencies;
3. Temperature dependence of resonance frequency equal to temperature dependence of sublattice magnetization;
4. Strong enhancement of NMR signal by factor η, i.e., resonance easy to detect;
5. Frequency pulling.

Knowing crystallographic and magnetic structures of a crystal one might find a general form of local fields on nuclei.

Assume that the local magnetic field on a nucleus of any magnetic sublattice depends linearly on an electron magnetic moment of its own atom as well as of surrounding atoms from all sublatices. Local fields on any nucleus from <math>\nu</math>-th sublattice is given by:

<math>{H}^{\alpha}_{n}(j_{\nu})=\sum_{\nu^{\prime}\j^{\prime}_{\nu^{\prime}}} {A}^{\alpha\beta}_{\j_{\nu}\j^{\prime}_{\nu^{\prime}}} {M}^{\beta}_{\j^{\prime}_{\nu^{\prime}}}.</math>

Here <math>\alpha \quad (\beta) \equiv {x,y,z}</math> (there is summation over β too), <math>{M}_{j_{\nu}}</math> - magnetic moment of the <math>{j_{\nu}}</math>-th atom (ion) normalized by corresponding atomic volume, <math>{A}^{\alpha\beta}_{\j_{\nu}\j^{\prime}_{\nu^{\prime}}}</math> are dimensionless coefficients, maximum number of which is given by a local symmetry of atomic nodes in the sublattice <math>\nu</math>. In the case of equivalent positions the corresponding coefficients can be obtained by symmetry transformation of the <math>\nu</math>-th sublattice.

The anisotropy of hyperfine interactions gives rise to the dependence of NMR frequency on position of nuclear spin in the domain wall.

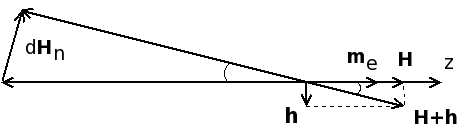
NMR method might be used to investigate the magnetocrystalline anisotropy in ferromagnetic films. The NMR enhancement factor η in a single-domain specimen is given by

<math> \eta(H)=\frac{\partial{H}^{\bot}_{n}}{\partial{h}}=-H_{n}\text{sin}(\phi+\theta_0)\left(\frac{\partial{\theta_0}}{\partial{h}}\right)_{h=0}. </math>

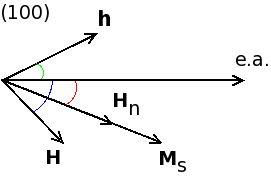
The angle θ₀ represents the equilibrium position of the electronic saturation magnetization vector M_S of a magnetically anisotropic sample, h is the rf field vector, φ is the angle between the easy magnetization axis and the vector h, H_n - vector of local field on nuclei.

The angle θ₀ can be found by minimizing the total magnetic energy. For example, assuming a biaxial magnetic anisotropy in the (100) film plane, with easy axis along [110] the total magnetic energy for an ideal cubic crystal is given by:

<math> E=K_{1}\sin^{2}\theta\cos^{2}\theta-HM_{s}\cos(\alpha-\theta)-hM_{s}\cos(\phi+\theta) </math>

where θ, φ, and α are angles between the easy magnetization axis and the vectors M_S, h, and H, respectively. Then for a resonant excitation of the nuclei in the domain bulk, the equation for η predicts the following field dependence for the echo amplitude:

<math> A(H,\alpha,\theta)=H_n\cdot\frac{\sin^{2}(\phi+\theta_{0})}{(2K_{1}/M_{s})\cos(4\theta_0)+H\cos(\alpha-\theta_{0})}+O(h) </math>

where θ₀ is the angular coordinate of the equilibrium magnetization.

So for fixed values of φ and α, it is possible to find the field dependence of the echo signal A(H); for fixed values of φ and H, it is possible to obtain the angular dependence A(α). The anisotropy field H_k=2K₁/M_S corresponds to the maximum of A(H), and the maxima of A(α) determine the directions of the difficult magnetization axes in a crystal.

1. Study of reference samples of known structure in order to gain the prior information on local hyperfine properties;
2. This information is used to determine, in structurally unkown systems, the probabilities to find the probed nuclei in the various phases or atomic configurations of the samples and the histogram of local environments;
3. To propose a 3D structure describing the arrangenment of atoms.

1. M.I. Kurkin and E.A. Turov, NMR in magnetically ordered materials and its applications (Nauka, Moscow, 1990) (in Russian),
2. E.A. Turov and M.P. Petrov, Nuclear Magnetic Resonance in Ferro- and Antiferromagnets (Halsted, New York, 1972).
3. P. Panissod, Structural and magnetic investigations of ferromagnets by NMR. Application to magnetic metallic multilayers, in Frontiers in Magnetism of Reduced Dimension Systems, V.G. Bar'yakhtar et al. (eds.) (Kluwer, Netherlands, 1998).
4. P.C. Riedi, T. Thomson and G.J. Tomka, NMR of thin magnetic films and superlattices, in Handbook of Magnetic Materials, Vol. 12, Edited by K.H.J. Buschow (Elsevier, 1999)
5. S. Wurmehl and J.T. Kohlhepp, Nuclear magnetic resonance studies of materials for spintronic applications, J. Phys. D: Appl. Phys 41 (2008) 173002