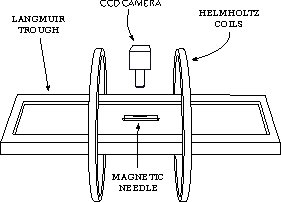
The instrument is designed to measure the mechanical response of a Langmuir monolayer to an external shear deformation. The instrument is a custom-made apparatus analogous to the one recently developed by the group of Gerald Fuller [@Brooks1999 @Reynaert2008].

The stress exerted by the needle on the film is equal to the shear oscillating force (with amplitude $F$), divided by two times the length $L$ of the magnetic needle. The resulting shear strain $\gamma$ is equal to the needle oscillation amplitude $X$, divided by the distance $W$ between the needle and the channel that delimits the investigated portion of the film. The oscillations of $\gamma$ and $\sigma$ are separated by a phase lag $\delta$. The dynamic modulus is then given by:

$$G(\omega)=\frac{\sigma(\omega)}{\gamma(\omega)}= \frac{W}{2L}\frac{F(\omega)}{X(\omega)}e^{i\delta}$$

This experimental technique presents some limitations, related to its intrinsic design. A measurement performed on a film characterized by a low value of $G$ may be strongly affected by contributions from the drag of the water subphase. At the same time, the technique is not suited to measure the response of very rigid films: the high force required to move the needle may induce undesired non-linear effects in the measurements of $G$.

The low limits of the dynamic range of the instrument is usually related to the so-called Boussinesq number, defined as the ratio between the drag due to the film at the interface, and the drag due to the subphase, that affect the movement of the needle at the interface. It is expressed as

$$B = \frac{d_{film}}{d_ {subphase}} = \frac{\eta_s \: P \: L_b}{\eta_b \: A \: L_s}$$

where $\eta_s$ and $\eta_b$ are the viscosities of the film and of the subphase, $A$ and $P$ are the area and the perimeter of the contact region between the needle and the film, $L_s$ and $L_b$ are the lengths over which the velocity fields vary in the film and in the bulk. Depending on the value of $B$, three regimes can be roughly identified:

• if $B \gg 1$, the effect of the subphase on the measurement of $G$ are negligible;

• if $B \ll 1$, the needle is probing the flow properties of the subphase;

• an intermediate regime for $B \simeq 1$, where the interpretation of the measurement of the shear modulus $G$ has to account in some way the contributions due to the drag of the subphase.

1. Instrument design and calibration
2. To operate the instrument, please follow this operation list.