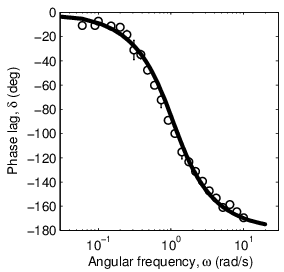Indice
Instrument design
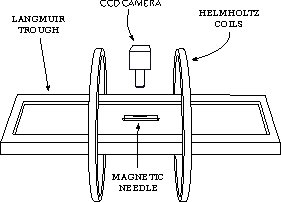
The interfacial rheometer we developed is an upgraded version of the instrument described by Fuller, adapted to the study of photosensitive polymers. A sketch and two photographs of the instrument are shown in the figure aside.
The instrument is build around the Langmuir trough described here. Two parallel glass plates, each of them $10cm$ long, define a channel used to constrain the needle position along the direction parallel to the short edge of the trough. The stainless steel needle is typically $13mm$ long and has a diameter of $0.35mm$; its surface is kept clean by immersion in chloroform. The needle is magnetized to saturation value before each experiment by contact with a permanent magnet.
Two coils in Helmholtz configuration (diameter $D=32cm$, resistance $R=7\Omega$) are placed around the Langmuir trough: each of them carries a static current $I_0 = 1 A$. The static magnetic field generated by $I_0$ aligns the needle along the axis of the coils, as shown in the figure below. The whole system is oriented parallel to the North-South direction, so the Earth field does not affect the alignment of the needle. A sinusoidal current is added to one of the coils, producing the oscillating field gradient that moves the needle. A typical sinusoidal wave of frequency $0.25Hz$ and amplitude $I=1mA$ generates a force $F$ of the order of $50nN$ on the needle, resulting in a displacement of about $10\mu m$.
This “two-coils” design is a simplification of the design originally proposed by Fuller and coworkers, which makes use of two coils in Helmholtz configuration to generate the static magnetic field, and two smaller coils in anti-Helmholtz configuration as the source of the oscillating magnetic gradient that moves the needle. In the following, we show that the use of two coils do not alter significantly the behavior of the oscillating magnetic field gradient, with respect to the one obtained with four coils.
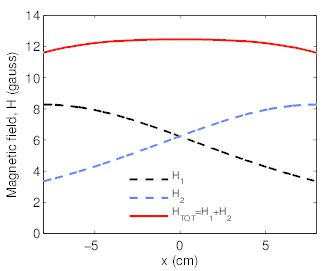
We name $x$ the distance from the center of the trough, along the axis of the two coils. Figure below, left panel reports the magnetic fields $H_1$ and $H_2$ generated by each coil -placed respectively at $x=-8cm$ and $x=8cm$- and by the two coils in Helmholtz configuration. Close to $x=0cm$, the total field $H_{tot}$ is constant over $x$. When the oscillating current $I$ is added to one coil, near to $x=0cm$ the field $H_{tot}$ grows linearly with $x$. If the needle, aligned parallel to the axis of the coils, is described as a magnetic dipole of momentum $\mu$, the force exerted on the needle is given by
$$\overrightarrow{F}(x) = \overrightarrow{\mu} \times \nabla \overrightarrow{H}(x)$$
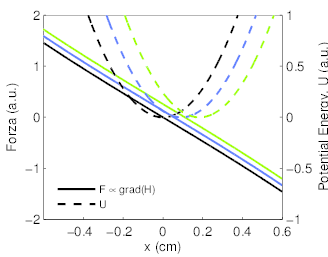
In the following, we consider only the component of the force parallel to the axis of the two coils. A calculation of the behavior of $F(x)$ for our instrument is shown in the central panel of the next figure. Close to $x=0$, $F$ is directly proportional to $x$: therefore, an elastic constant can be defined as
$$k=\frac{F(x)}{x}.$$
Given this linearity, the energy of the dipole-field interaction $U(x)$ is parabolic in proximity of $z=0$. The needle will change its position accordingly to the position $x_0$ of the minimum of $U$. Since $x_0$ depends on the value of the oscillating current $I$, we have that
$$x_0 = A e^{i\omega t}.$$
One may consider that, while in the four-coils configuration the value $k$ is constant, this do no happen in a two-coils design.
The calculation reported in the previous figures shows that the dependence of $k$ over the current $I$ is negligible in the present experimental setup; the relative variation of $k$ reaches a maximum value of the order of $10^{-3}$.
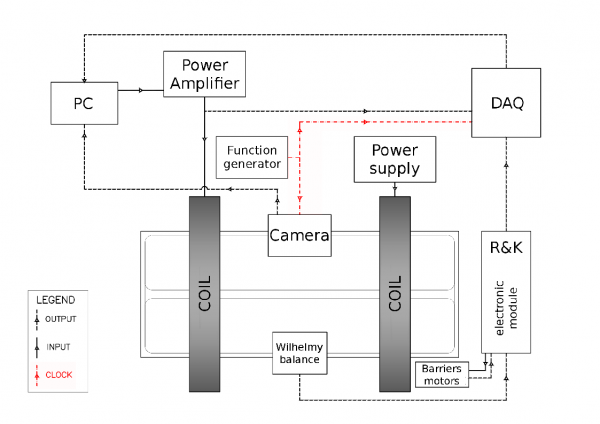
The resulting displacement $d(\omega)$ of the needle -of the order of $50\mu m$- is detected by a CCD camera [1] equipped with a long focal objective [2]. An hardware DAQ board [3] is used to control the instrument: using its analog outputs it is possible to drive the trough barriers and to apply the oscillating current to the Helmholtz coils via a set of power supplies. The DAQ analog inputs are used to measure the trough area, the surface pressure and the current on the coils as functions of time. Both the DAQ hardware board and the CCD camera are triggered by an external reference wave, oscillating at 14Hz. The external triggering is needed to properly measure the phase lag $\delta(\omega)$ between stress and strain, ensuring that the correct mechanical response is retrieved. A connection scheme of the experimental setup is sketched in the figure below: the connections relative to the trigger signal are depicted in red.
- The Imaging Source, 1024x768 pixels
- Mitutoyo MPLAN-APO-20X
- National Instruments PCI-6036e
Calibration: oscillations on pure water
In order to characterize the inertial response of the needle, we consider the oscillatory movement of the needle on a pure water surface. The total force exerted on the needle given by the composition of:
a) a viscous drag force $F_c = -d \dot{x}$, where $d$ is the drag coefficient for a motion parallel to the axis of the needle. If the needle is thin - its radius is much shorter than its length ($a \ll L$)- then the drag coefficient is given by a relatively simple expression @Levine2004
$$d= \frac{2 \pi \eta L}{\log \left( 0.43 L/l_0 \right)}$$
The drag coefficient $d$ is then related to the water viscosity $\eta$, the needle length $L$ and a characteristic length $l_0$ over which the two dimensional fluid velocity field can vary, which can be safely assumed to be of the order of the needle’s radius $a$;
b) an harmonic force originating from the interaction between the magnetic dipole of the needle and the magnetic field gradient generated by the system of coils,
$$F_m = -k \left( x-x_0 \right) = - \frac{\partial^2 U}{\partial x^2} \left( x-x_0 \right)$$
where k is the elastic constant previously defined and U is the energy of the dipole-field interaction. The center $x_0$ of the harmonic potential oscillates with angular frequency $\omega$ (see equation [eq:cenharm]).
The resulting differential equation is
$$m \ddot{x} = - d\dot{x} -kx + kAe^{i\omega t}$$
This equation is that of a forced-dumped oscillator of mass $m$, spring constant $k$ and damping constant $d$ @Reynaert2008. The ratio $AR$ of the amplitudes of the needle and force oscillation, and the phase lag $\delta$ result as:
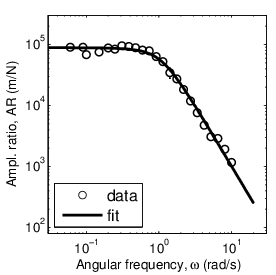
$$AR=\frac{X}{kA}=\frac{1}{\sqrt{(k-m\omega^2)^2+(\omega d)^2}}$$
$$\delta=\arctan \left( \frac{-\omega d}{k-m \omega^2} \right)$$
Commonly, instead of measuring the elastic constant $k$, the simpler approach of measuring the oscillatory voltage $V$ applied to one of the two coils is preferred. Therefore, a calibration constant has to determined; in order to do that, the amplitude ratio $AR_V=\frac{X}{V}$ is measured. Observing the high-frequency limit of $AR$, it can be noted that it is proportional to $\omega^2$ via the mass of the needle $m$.
$$\frac{X(\omega)}{F(\omega)} = \frac{X(\omega)}{\alpha V(\omega)} \rightarrow {m \omega^2}, \; \omega \rightarrow \infty$$
This relation -in analogy with @Brooks1999- allow the determination of the *calibration constant* $\alpha$:
$$\alpha = \frac{1}{m\omega^2}\lim_{\omega \rightarrow \infty}{\frac{X}{V}}$$
A measurement of $AR$ and $\delta$ is reported in the figure below in logarithmic and semilogarithmic scale, respectively.
While the mass $m$ of the needle is measured, the oscillator parameters $k$ and $d$ were determined by a fit performed on the stress-stain ratio curve using equation [eq:isr-amplratio]; they are reported in table [tab:kmd]. The phase lag $\delta$ is in very good agreement with the model curve built from the parameters of table [tab:kmd] (figure [fig:isr-water]b) using equation [eq:isr-phase].
| $k$ | $1.13 \cdot 10^{-5} N/m$ |
|---|---|
| $m$ | $ 9.9 \cdot 10^{-6} Kg$ |
| $d$ | $1.74 \cdot 10^{-5} Kg/s$ |
It is worth comparing the value of $d$ obtained from the fit of the experimental curves with its theoretical value calculated using equation [eq:drag]. If the characteristic length $l_0$ is taken equal to the needle’s radius $a$, we obtain $d_t=2.38 \cdot 10^{-5} Kg/s$, with respect to the measured value of $1.74 \cdot 10^{-5} Kg/s$: the order of magnitude of the drag is correctly predicted.
Oscillations in presence of a film
The presence of a film at the air/water interface induces an additional hindrance of the motion of the needle, thus reducing the amplitude of its oscillations and modifying the phase lag between stress and strain.
An measurement of the response of a Langmuir film can be considered meaningful is it is significantly different from the measurement performed in absence of film, which characterize the intrinsic oscillating behavior of the system. If this deviation is too small, than the measurement is likely to include huge effects due to the drag of the subphase.
As stated at the beginning of this chapter, the contribution to the drag due to the water subphase are negligible if the Boussinesq number $B$ is high: $B»1$.
Usually, a so-called *experimental Boussinesq number* @Brooks1999 [@Reynaert2008]
$$B_{exp} = \frac{AR_{sys}}{AR_{film}}$$
is used in the literature to quantify the deviation of the response of the needle from the behavior observed on pure water. If $B_{exp} > 10-100$ in the frequency range investigated, then the mechanical response measured may be considered as not affected by hydrodynamic contributions due to the bulk of the subphase. In this case, the shear modulus $G$ is given by
$$G(\omega) = \frac{W}{2L}\frac{\alpha V(\omega)}{X(\omega)} e^{i\delta}$$
If $B \simeq 1$, the subphase drag contribution to $G$ has to be decoupled from the one due to the film. A simple way to decouple the contributions to $G$ arising from the drag of the film and from the drag of the subphase, when the latter is not negligible, is to imply a linear relation between the two quantities @Brooks1999a [@Reynaert2008], so that
$$G_{film}= G_{meas}- G^*_{water} =G_{meas} - \frac{W}{2L}AR_{w} \exp{(i\delta_{w})}.$$
The accuracy of this procedure is questionable. In this work, the preferred approach consists in setting a confidence threshold value $B_{exp} = 10$, above which the measurement can be considered as not influenced by subphase drag contributions.
Measuring the response of a Newtonian fluid
An additional control of the instrument calibration is conducted measuring the response of films of poly(dimethylsiloxane) of controlled thickness $d$ and known viscosity $\eta_ {bulk}=0.97 Pa\cdot s$. This oil has the mechanical response of an ideal (newtonian) fluid: it presents a purely viscous response with frequency-independent shear viscosity $\eta_s$.
In case of predominantly viscous systems, the generalized viscosity $\eta_{2D}$ is obtained from $G$ through the simple relation:
$$\eta_{2D}=\frac{G"}{\omega}.$$
It is reasonable to assume that $\eta_{2D}$ is proportional to the bulk viscosity through the thickness of the film, $\eta_{2D}= d \cdot \eta_{bulk}$, thus ignoring confinement effects.
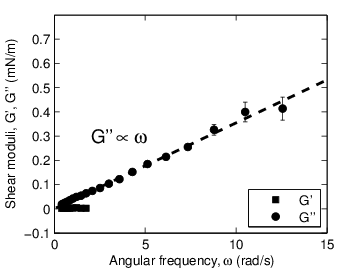
Data are shown in figure above, left panel: the film behaves as a Newtonian fluid with $G"$ (circles) growing linearly with the frequency, as indicated by fit represented by the dashed line, while $G'$ is zero within the error. On the right we compare the value of the viscosity $\eta_{2D}$ obtained from $G''$ for each film thickness d with its expected value based on the bulk viscosity.
The results are consistent with the theoretical behavior for an ideal viscous fluid. However, careful inspection of the data from the lowest thickness ($d<50\mu m$, represented by the gray area in the picture) shows a small deviation which can be ascribed to the drag due to the water subphase, which becomes comparable to that of the film when this becomes too thin. This effect has already been found and discussed in the literature @Reynaert2008. If we suppose, in a simple approximation, a linear superposition of these effects, a rough estimate of the subphase drag is obtained: $|G|_{sub} \simeq 10 \mu N/m$.
Adaptation for photosensitive polymers
The study of the mechanical properties of photosensitive polymers requires a proper adaptation of the instrument described so far. In particular, the instrument had to be enclosed in an aluminum box equipped with removable walls, to ensure that spurious light from the ambient does not influence the rheological properties of the film. Moreover, the illumination light required for the tracking of the needle’s position has to be chosen in a spectral region where the sample is characterized by low absorbance. For the photosensitive azopolymers investigated in this work, red light ($\lambda >630nm$) was chosen.